Study of a Centrifugal Pump Characteristic Curve

Context: Fluid MechanicsThe branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them. and TurbomachineryMachines that transfer energy between a rotor and a fluid, including both turbines and pumps..

In industrial pressurized hydraulic networks, selecting the right pump is critical. The performance of a centrifugal pump is described by its Characteristic Curves (Head vs. Flow). This exercise focuses on determining the Operating Point of a pump within a specific piping system and calculating its efficiency and power requirements using US Customary Units.

Pedagogical Note: This exercise will teach you how to match a pump curve with a system curve to find the flow rate in a network, and how to compute hydraulic power (\(P_{\text{h}}\)) and Brake Horsepower (\(\text{BHP}\)).

Learning Objectives

Understand the H-Q (Head-Flow) curve of a centrifugal pump.
Establish the System Curve equation based on static head and friction losses.
Determine the Operating Point (Intersection of Pump and System curves).
Calculate Hydraulic Power and required Motor Power (\(\text{BHP}\)).

Study Data

A centrifugal pump is installed to transfer water at 60°F from a lower reservoir to an elevated tank.

System Specifications

Characteristic	Value
Fluid	Water (SG = 1.0)
Pump Type	Centrifugal, variable flow
Piping System	Steel Pipe, Sched 40

Schematic of the Pumping System

Parameter	Symbol	Value	Unit
Pump Curve Equation	\(H_{\text{pump}}(Q)\)	\(120 - 0.004 \cdot Q^2\)	H in ft, Q in gpm
Static Head (Elevation Diff.)	\(H_{\text{static}}\)	50	ft (feet)
System Friction Coefficient	\(k\)	0.003	ft / gpm²
Pump Efficiency at Opt. Point	\(\eta\)	75	%

Questions to Address

Write the equation for the System Curve \(H_{\text{sys}}(Q)\).
Determine the Operating Point (Flow Rate \(Q_{\text{op}}\) and Total Head \(H_{\text{op}}\)).
Calculate the Hydraulic Power (\(P_{\text{h}}\)) delivered to the fluid.
Calculate the required Brake Horsepower (\(\text{BHP}\)) for the motor.
Conclusion on pump selection.

Fundamentals of Pump Hydraulics

The performance of a pump in a circuit is determined by the interaction between the pump's capability and the system's resistance.

1. System Curve
The Total Dynamic Head (TDH) required by the system is the sum of the static lift and the friction losses (head loss) which vary with the square of the flow rate: \[ H_{\text{sys}} = H_{\text{static}} + k \cdot Q^2 \]

2. Operating Point
The pump operates where its performance curve intersects the system curve: \[ H_{\text{pump}} = H_{\text{sys}} \]

3. Power Formulas (US Units)
Hydraulic Power (in Horsepower): \[ P_{\text{h}} (\text{hp}) = \frac{Q (\text{gpm}) \cdot H (\text{ft}) \cdot \text{SG}}{3960} \] Brake Horsepower (Power required at the shaft): \[ \text{BHP} (\text{hp}) = \frac{P_{\text{h}}}{\eta_{\text{pump}}} \]

Solution: Study of a Centrifugal Pump Characteristic Curve

Question 1: System Curve Equation

Principle

The system curve represents the energy required to move fluid through the pipe. It consists of a static component (elevation) and a dynamic component (friction) that increases with flow.

Mini-Lesson

The Static Head (\(H_{\text{static}}\)) is the vertical distance the fluid must be lifted. Friction Losses (\(h_{\text{f}}\)) depend on pipe length, diameter, roughness, and fittings. This relationship is often simplified to \(h_{\text{f}} = k \cdot Q^2\).

Pedagogical Note

Visualize this as the "demand" of the pipe network. Even at zero flow, you still need enough pressure just to hold the water column up (50 ft).

Norms

Friction factors are typically determined using the Darcy-Weisbach equation and Moody Diagram, or empirical formulas like Hazen-Williams, compliant with ANSI/ASME B31 standards for pressure piping.

Formula(s)

The general system curve equation:

H_{\text{sys}}(Q) = H_{\text{static}} + k \cdot Q^2

Hypotheses

We assume incompressible flow (water), fully developed turbulent flow (justifying the squared relationship), and that the reservoirs are large enough that their levels remain constant.

Data

From the study data:

Parameter	Symbol	Value	Unit
Static Head	\(H_{\text{static}}\)	50	ft
Friction Coeff.	\(k\)	0.003	\(\text{ft}/\text{gpm}^2\)

Tips

Ensure your units for \(k\) match the flow rate units squared. Here, \(k\) is in \(\text{ft}/\text{gpm}^2\), so \(Q\) must be in \(\text{gpm}\).

Schematic (Before Calculations)

The system curve starts at \(H_{\text{static}}\) on the Y-axis and curves upward.

System Curve Concept

Calculation(s)

We substitute the known values directly into the standard formula:

1. Identify variables: \(H_{\text{static}} = 50\), \(k = 0.003\).

2. Substitute into the equation:

\begin{aligned} H_{\text{sys}}(Q) &= H_{\text{static}} + k \cdot Q^2 \\ H_{\text{sys}}(Q) &= 50 + 0.003 \cdot Q^2 \end{aligned}

This equation gives the required head in feet for any given flow Q in gpm.

Schematic (After Calculations)

Here is a graphical representation of the function we just established.

Analysis

The equation shows that doubling the flow rate (\(Q\)) will quadruple the friction loss term (\(0.003 \cdot Q^2\)). This is why pumping faster costs significantly more energy.

Cautionary Points

Do not confuse Pressure Head with Static Head. Static head is purely elevation difference. Pressure head would be added if the discharge tank was pressurized.

Key Takeaways

System Head = Static Head + Dynamic Head (Friction).
Static head is independent of flow rate.

Did You Know?

Over time, pipes corrode and scale builds up. This increases the friction factor \(k\), making the system curve steeper and reducing flow rate as the installation ages.

FAQ

Common questions about system curves:

Final Result

\(H_{\text{sys}}(Q) = 50 + 0.003 \cdot Q^2\)

Your Turn

If the flow rate Q is 50 gpm, what is the required system head?

Memo Card

Formula: \(H_{\text{sys}} = H_{\text{stat}} + h_{\text{f}}\)

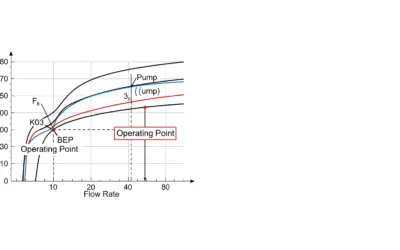
Question 2: Operating Point Determination

Principle

The operating point is the unique state of equilibrium where the pump supplies exactly as much energy as the system consumes.

Mini-Lesson

The pump curve (\(H_{\text{pump}}\)) slopes downward (less head at higher flow). The system curve (\(H_{\text{sys}}\)) slopes upward (more resistance at higher flow). The intersection defines the natural Operating Point.

Pedagogical Note

Always ensure units are consistent before setting equations equal. Here, both equations output Head in feet (ft) for Flow in gallons per minute (gpm).

Norms

The Hydraulic Institute (HI) standards define how these curves are generated and verified during factory testing, ensuring predicted performance matches reality.

Formula(s)

H_{\text{pump}}(Q) = H_{\text{sys}}(Q)

120 - 0.004 \cdot Q^2 = 50 + 0.003 \cdot Q^2

Hypotheses

We assume the pump runs at a constant speed (RPM) and fluid properties (viscosity/density) remain constant during operation.

Data

\(\text{Pump Curve}: 120 - 0.004 Q^2\)
\(\text{System Curve}: 50 + 0.003 Q^2\)

Tips

Graphing the two curves is a great way to sanity-check your calculated result. The intersection must lie on both lines.

Schematic (Before Calculations)

Intersection Concept

Calculation(s)

We solve for flow rate \(Q\) step-by-step:

1. Equate Pump Head and System Head:

120 - 0.004 \cdot Q^2 = 50 + 0.003 \cdot Q^2

2. Group constants on the left and \(Q\) terms on the right:
Subtract 50 from both sides and add \(0.004 Q^2\) to both sides.

\begin{aligned} 120 - 50 &= 0.003 \cdot Q^2 + 0.004 \cdot Q^2 \\ 70 &= 0.007 \cdot Q^2 \end{aligned}

3. Isolate \(Q^2\):
Divide both sides by 0.007.

\begin{aligned} Q^2 &= \frac{70}{0.007} \\ Q^2 &= 10,000 \end{aligned}

4. Solve for \(Q\):

Q = \sqrt{10,000} = 100 \text{ gpm}

5. Calculate Head (\(H_{\text{op}}\)):
Substitute \(Q=100\) back into the pump equation (or system equation).

\begin{aligned} H_{\text{op}} &= 120 - 0.004 \cdot (100)^2 \\ &= 120 - 0.004 \cdot 10,000 \\ &= 120 - 40 \\ &= 80 \text{ ft} \end{aligned}

We find that the system balances at a flow of 100 gpm and a head of 80 ft.

Schematic (After Calculations)

Resulting Operating Point

Analysis

The pump will naturally settle at 100 gpm. If you need more flow, you must increase pump speed (RPM) or reduce system friction (\(k\)) by using larger pipes or opening valves.

Cautionary Points

If the calculated \(Q^2\) is negative, it means the Static Head is higher than the Pump's Shut-off Head (120 ft). In that case, flow is zero.

Key Takeaways

The operating point is NOT determined by the pump alone.
It is the intersection \(H_{\text{pump}} = H_{\text{sys}}\).

Did You Know?

Variable Frequency Drives (VFDs) allow you to change the pump speed, effectively shifting the red curve up or down to change the operating point dynamically.

FAQ

Common questions about operating points:

Final Result

\(Q_{\text{op}} = 100 \text{ gpm}\), \(H_{\text{op}} = 80 \text{ ft}\).

Your Turn

If the pump speed increased such that the curve became \(H = 150 - 0.004Q^2\), would the flow rate increase or decrease?

Memo Card

Concept: Intersection of Supply (Pump) and Demand (System).

Question 3: Hydraulic Power Calculation

Principle

Hydraulic power (\(P_{\text{h}}\) or WHP - Water Horsepower) represents the rate at which useful energy is transferred to the fluid by the pump.

Mini-Lesson

Power is Work/Time. In hydraulics, it scales linearly with Flow (\(Q\)), Head (\(H\)), and Density (\(\text{SG}\)). The constant 3960 is a conversion factor for US units (\(33,000 \text{ ft}\cdot \text{lb}/\text{min}\) per HP divided by the weight of a gallon of water \(\approx 8.33 \text{ lb}\)).

Pedagogical Note

Think of Hydraulic Power as the "ideal" power output. It assumes no losses inside the pump.

Norms

Power calculations follow ANSI/HI 1.3 standards for centrifugal pumps. It defines the density of water at various temperatures for precise calculations.

Formula(s)

P_{\text{h}} = \frac{Q \cdot H \cdot \text{SG}}{3960}

Hypotheses

We assume the fluid is water with a Specific Gravity (\(\text{SG}\)) of 1.0, which is standard for cold water (approx 60°F).

Data

From Question 2:

Parameter	Value	Unit
Flow (\(Q\))	100	gpm
Head (\(H\))	80	ft
Specific Gravity (\(\text{SG}\))	1.0	-

Tips

Common mistake: Do not use the pump's maximum flow or maximum head. You must use the Q and H at the Operating Point calculated in Step 2.

Schematic (Before Calculations)

Calculation(s)

We break the fraction down:

1. Calculate the numerator (Work factor):

\begin{aligned} \text{Numerator} &= Q \cdot H \cdot \text{SG} \\ &= 100 \cdot 80 \cdot 1.0 \\ &= 8000 \end{aligned}

2. Divide by the conversion constant:

P_{\text{h}} = \frac{8000}{3960}

3. Final Result:

\begin{aligned} P_{\text{h}} &\approx 2.0202... \\ &\approx 2.02 \text{ hp} \end{aligned}

This value represents the theoretical power required if the pump was perfectly efficient.

Schematic (After Calculations)

The value of 2.02 hp represents the pure energy gain of the water column.

Analysis

This 2.02 hp is the raw energy gained by the water. It does not account for the pump's mechanical losses yet.

Cautionary Points

If you are pumping oil or brine, \(\text{SG}\) will not be 1.0, significantly changing the power requirement.

Key Takeaways

\(P_{\text{h}}\) depends on Q, H, and Fluid Density.
It is independent of pump efficiency.

Did You Know?

1 Horsepower equals 550 foot-pounds per second. In electrical terms, 1 hp is approximately 746 Watts.

FAQ

Common questions about power calculations:

Final Result

\(P_{\text{h}} \approx 2.02 \text{ hp}\).

Your Turn

Calculate \(P_{\text{h}}\) if Q = 200 gpm and H = 40 ft.

Memo Card

Formula: \(P_{\text{h}} = \frac{Q \cdot H}{3960}\) (for water)

Question 4: Brake Horsepower (BHP)

Principle

BHP is the power the motor must deliver to the pump shaft. It is always higher than hydraulic power because pumps are not 100% efficient; energy is lost to friction, turbulence, and leakage.

Mini-Lesson

Efficiency (\(\eta\)) is the ratio of useful output to total input: \(\eta = \frac{\text{Output}}{\text{Input}} = \frac{P_{\text{h}}}{\text{BHP}}\). Therefore, \(\text{BHP} = \frac{P_{\text{h}}}{\eta}\).

Pedagogical Note

The motor must be "stronger" than the water needs. Efficiency acts as a penalty factor on the input side.

Norms

Motors are typically sized according to NEMA standards (e.g., 1, 1.5, 2, 3, 5, 7.5 hp...). We typically select the next standard size up from our calculated BHP to provide a safety margin (Service Factor).

Formula(s)

\text{BHP} = \frac{P_{\text{h}}}{\eta}

Hypotheses

We assume the efficiency given (75%) is accurate for the calculated operating point (\(Q=100\) gpm). In reality, efficiency varies with flow.

Data

Hydraulic Power \(P_{\text{h}} = 2.02\) hp.
Efficiency \(\eta = 75\% = 0.75\).

Tips

Always check your result: BHP must be greater than \(P_{\text{h}}\). If it's smaller, you multiplied by efficiency instead of dividing.

Schematic (Losses)

Cautionary Points

Do not confuse Motor Efficiency with Pump Efficiency. We are using Pump Efficiency here to find shaft power.

Calculation(s)

Substitute the known values:

\begin{aligned} \text{BHP} &= \frac{2.02}{0.75} \\ &= 2.6933... \\ &\approx 2.69 \text{ hp} \end{aligned}

This means the motor must provide 2.69 hp to the shaft.

Schematic (After Calculations)

The 2.69 hp represents the input requirement.

Analysis

The calculation shows we need 2.69 hp at the shaft. A standard 2 hp motor would be overloaded and likely trip or burn out. The next standard NEMA size is 3 hp.

Key Takeaways

Efficiency \(\eta < 1.0\).
Input > Output.
Motor sizing requires rounding up.

Did You Know?

Oversizing motors too much (e.g., using a 10 hp motor here) reduces the Power Factor of the plant's electrical system, which can lead to utility fines.

FAQ

Common questions about motor sizing:

Final Result

\(\text{BHP} \approx 2.69 \text{ hp}\).

Memo Card

Key Relationship: \(\text{BHP} = P_{\text{h}} / \eta\).

Your Turn

If the pump were only 50% efficient, what BHP would be required for the same hydraulic power (2.02 hp)?

Question 5: Conclusion

Principle

A final engineering conclusion summarizes the operating conditions, confirms equipment suitability, and suggests final specifications.

Mini-Lesson

Pump selection involves checking flow, head, power, and efficiency. Operating near the BEP (Best Efficiency Point) ensures longevity and energy savings.

Pedagogical Note

Engineering is about making a decision. Is this pump "Good" or "Bad"? Based on 75% efficiency, it seems like a good selection.

Norms

Final reporting should comply with project documentation standards (e.g., ISO 9001). Proper labeling and documentation of the selected motor size are crucial for maintenance.

Hypotheses

We assume the motor selected (3 hp) matches the pump speed and frame size and that the service factor provides additional safety.

Data

Summary of Findings:
- Q: 100 gpm
- H: 80 ft
- BHP: 2.69 hp
- Efficiency: 75%

Tips

Always document your operating point. If the system changes later (new pipes, new tank), you can compare against this baseline to troubleshoot.

Schematic (Final Overview)

Final Selection Visualization

Calculation(s)

We verify the safety margin with the selected 3 HP motor:

\begin{aligned} \text{Margin} &= \frac{\text{Rated Power} - \text{Required Power}}{\text{Required Power}} \\ &= \frac{3.0 - 2.69}{2.69} \\ &= \frac{0.31}{2.69} \\ &\approx 0.115 \quad (11.5\%) \end{aligned}

This 11.5% margin is safe for typical industrial applications.

Schematic (After Calculations)

This visual confirms the motor has excess capacity.

Analysis

We have successfully sized the operation. The Flow Rate of 100 gpm meets the system needs. The Power requirement of 2.69 hp is well covered by a 3 hp motor. Operating at 75% efficiency suggests the pump is well-matched to this application, minimizing energy waste and heat generation.

Cautionary Points

Ensure NPSHa (Available Net Positive Suction Head) is calculated separately to prevent cavitation, although not covered in this specific exercise.

Key Takeaways

The operating point is dynamic.
Motor sizing is discrete (standard steps).

Did You Know?

Energy costs often exceed the purchase price of the pump within the first year of continuous operation.

FAQ

Common questions about system design:

Final Result

The system operates at 100 gpm / 80 ft with a 3 hp motor.

Memo Card

Summary: 100 gpm @ 80 ft, 3 HP Motor.

Your Turn

Is a 2.5 hp motor sufficient for this application?

Interactive Tool: Pump & System Matcher

Adjust the system parameters to see how the Operating Point shifts along the Pump Curve.

System Parameters

Static Head (\(H_{\text{static}}\)) 50 ft

Friction Coeff. (\(k\)) 0.003 ft/gpm²

Operating Point

Operating Flow (\(Q_{\text{op}}\)) -

Operating Head (\(H_{\text{op}}\)) -

Final Quiz: Test Your Knowledge

1. What happens to the operating point if you partially close a discharge valve?

The friction curve becomes flatter, increasing flow.
The friction curve becomes steeper, decreasing flow.
The static head increases.

Closing a valve increases resistance (k), making the system curve steeper.

2. What is the "Shut-off Head" of the pump in this exercise?

120 ft
50 ft
100 ft

Shut-off head occurs at Q=0. From the equation \(H = 120 - 0.004Q^2\), if Q=0, H=120.

3. Why is Brake Horsepower (BHP) always higher than Hydraulic Power (\(P_{\text{h}}\))?

Because of fluid friction in the pipe.
Because of static head.
Because of mechanical and hydraulic losses within the pump.

Pump efficiency accounts for internal losses, requiring the motor to supply more power than what is transferred to the fluid.

Glossary

BEP (Best Efficiency Point): The flow rate at which the pump operates at its maximum efficiency. Operating far from BEP causes vibration and cavitation.
Head (H): The height to which a pump can raise a fluid, measured in feet (US) or meters (SI). It is a measure of pressure energy.
NPSH (Net Positive Suction Head): The margin between the liquid's pressure at the suction nozzle and its vapor pressure. Sufficient NPSH is required to prevent cavitation.