Hydraulic Learning

Comparison of Hydraulic Head Loss

Exercise: Comparing Hydraulic Head Loss

Comparison of Hydraulic Head Loss

Context: Fundamentals of Pressurized Pipe Flow.

Transporting fluids in pipes is a pillar of civil and industrial engineering. However, as a fluid flows, it inevitably loses energy due to friction against the pipe walls (friction head lossDecrease in fluid pressure (head) during flow, due to friction on the pipe walls. Also known as linear or major loss.) and disturbances caused by pipe fittings like elbows, valves, or contractions (minor head lossEnergy loss due to flow disruption at a specific location, such as an elbow, valve, or tee. Also known as singular loss.). Calculating these losses accurately is crucial for correctly sizing pumps and ensuring the desired flow rate. This exercise aims to quantify and compare these two types of losses in simple network configurations.

Pedagogical Note: This exercise will teach you to break down a hydraulics problem, identify the different sources of energy loss, and apply the fundamental formulas to evaluate them. You will see the concrete impact that fittings can have on the total energy loss of a network.

Learning Objectives

  • Differentiate and calculate friction (major) and minor head losses.
  • Calculate the Reynolds numberA dimensionless quantity that characterizes the flow regime of a fluid (laminar, transitional, or turbulent). to determine the flow regime.
  • Determine the Darcy friction factor using the Colebrook-White equation.
  • Apply the Darcy-Weisbach equation to calculate friction head loss.
  • Evaluate the impact of fittings (elbows, valves) on total head loss.

Problem Data

We want to compare the head loss for water flowing in two PVC piping configurations, each with a total length of 160 feet. The flow rate is constant.

Configuration Diagram
System A: Straight Pipe L = 160 ft System B: Pipe with Fittings 90° Elbow Valve 90° Elbow L_total = 160 ft 4.0" Diameter 4.0" Diameter
Characteristic Symbol Value Unit
Fluid - Water -
Water Temperature \(T\) 68 °F
Kinematic Viscosity of Water \(\nu\) \(1.08 \times 10^{-5}\) \(\text{ft}^2/\text{s}\)
Density of Water \(\rho\) 1.938 \(\text{slug}/\text{ft}^3\)
Flow Rate \(Q\) 320 \(\text{GPM}\)
Internal Pipe Diameter \(D\) 4.0 \(\text{in}\)
Total Pipe Length \(L\) 160 \(\text{ft}\)
Roughness of PVC \(k\) \(5 \times 10^{-6}\) \(\text{ft}\)
Loss Coefficient (90° Elbow) \(K_{\text{elbow}}\) 0.9 -
Loss Coefficient (Open Valve) \(K_{\text{valve}}\) 0.2 -

Questions

  1. Calculate the flow velocity and the Reynolds number. Is the flow laminar or turbulent?
  2. Determine the Darcy friction factor \(f\).
  3. Calculate the friction (major) head loss \(h_f\) for a length of 160 ft.
  4. Calculate the total minor head loss \(h_m\) for System B (which includes 2 elbows and 1 valve).
  5. Calculate the total head loss for each system and express the increase due to the fittings as a percentage.

Head Loss Fundamentals

1. Reynolds Number (\(Re\))
This dimensionless number compares inertial forces to viscous forces. It determines the flow regime:

  • \(Re < 2000\): Laminar flow (ordered, smooth flow).
  • \(Re > 4000\): Turbulent flow (chaotic flow, the most common case in engineering).
\[ Re = \frac{V \cdot D}{\nu} \] Where \(V\) is velocity, \(D\) is diameter, and \(\nu\) is kinematic viscosity.

2. Friction (Major) Head Loss (\(h_f\))
This is the energy lost due to the fluid's friction along the length of the pipe. It is calculated with the Darcy-Weisbach equation: \[ h_f = f \frac{L}{D} \frac{V^2}{2g} \] Where \(f\) is the Darcy friction factor, \(L\) is length, \(D\) is diameter, \(V\) is velocity, and \(g\) is the acceleration of gravity (\(32.2 \text{ ft/s}^2\)).

3. Darcy Friction Factor (\(f\))
In turbulent flow, this coefficient depends on both the Reynolds number and the relative roughness (\(k/D\)). It is determined by the implicit Colebrook-White equation, which is often solved iteratively or using a Moody diagram. \[ \frac{1}{\sqrt{f}} = -2 \log_{10}\left(\frac{k/D}{3.7} + \frac{2.51}{Re \sqrt{f}}\right) \]

4. Minor Head Loss (\(h_m\))
This loss is generated by localized obstacles (fittings). Each fitting is characterized by a loss coefficient \(K\). \[ h_m = K \frac{V^2}{2g} \] The total minor loss is the sum of the losses from each fitting: \(h_{m, \text{total}} = \left(\sum K_i\right) \frac{V^2}{2g}\).

Solution: Comparison of Hydraulic Head Loss

Question 1: Flow Velocity and Reynolds Number

Principle

The first step is to determine the basic characteristics of the flow. Velocity is directly related to the flow rate and the pipe's cross-sectional area. The Reynolds number will then tell us the nature of the flow (laminar or turbulent), which is essential for choosing the correct method to calculate the friction factor.

Mini-Lesson

The continuity equation (\(Q=V \times A\)) expresses the conservation of mass for an incompressible fluid: flow rate is the product of velocity and area. The Reynolds number physically compares inertial forces (which tend to create chaos, i.e., turbulence) to viscous forces (which tend to dampen motion and keep it orderly).

Pedagogical Note

Always start a hydraulics problem with these two calculations. They set the stage. Knowing whether the flow is laminar or turbulent is like knowing the rules of a game before you start playing: it dictates all subsequent steps.

Standards

The Reynolds number transition thresholds (typically 2000 for the end of laminar flow and 4000 for the beginning of turbulent flow) are universally accepted conventions in fluid mechanics and are cited in nearly all technical manuals and standards in the field.

Formula(s)

Velocity Formula

\[ V = \frac{Q}{A} \quad \text{with} \quad A = \frac{\pi D^2}{4} \]

Reynolds Number Formula

\[ Re = \frac{V \cdot D}{\nu} \]
Assumptions

For these initial calculations, we make the following assumptions:

  • The flow is incompressible (density \(\rho\) is constant).
  • The flow is uniformly distributed across the pipe's cross-section (we use average velocity).
  • The pipe is flowing full.
Given Data
ParameterSymbolValueUnit
Flow Rate\(Q\)320\(\text{GPM}\)
Internal Diameter\(D\)4.0\(\text{in}\)
Kinematic Viscosity\(\nu\)\(1.08 \times 10^{-5}\)\(\text{ft}^2/\text{s}\)
Tips

To quickly check your calculations, keep in mind that for common water distribution applications, pipe velocities are generally between 5 and 8 ft/s. Our result is in this range, which gives us confidence in the calculations.

Diagram (Before Calculations)

The following diagram illustrates the variables used to calculate velocity and Reynolds number in a pipe section.

Flow Parameters
V, QD
Calculation(s)

Flow Rate Conversion

First, we convert all units to standard USCU for calculations: Gallons Per Minute (GPM) to cubic feet per second (ft³/s).

\[ \begin{aligned} Q &= 320 \text{ GPM} \times \left(\frac{0.002228 \text{ ft}^3/\text{s}}{1 \text{ GPM}}\right) \\ &= 0.713 \text{ ft}^3/\text{s} \end{aligned} \]

The flow rate to be used in the formulas is 0.713 ft³/s.

Diameter Conversion

We do the same for the diameter, converting it from inches (in) to feet (ft).

\[ \begin{aligned} D &= 4.0 \text{ in} \times \left(\frac{1 \text{ ft}}{12 \text{ in}}\right) \\ &= 0.333 \text{ ft} \end{aligned} \]

The diameter is 0.333 ft.

Cross-Sectional Area (A) Calculation

Now that we have the diameter in feet, we calculate the area of the circular pipe using the formula \(A = \pi D^2 / 4\).

\[ \begin{aligned} A &= \frac{\pi D^2}{4} \\ &= \frac{\pi \times (0.333 \text{ ft})^2}{4} \\ &\approx 0.0871 \text{ ft}^2 \end{aligned} \]

The cross-sectional area for the flow is approximately 0.0871 ft².

Velocity (V) Calculation

The average velocity (V) is the flow rate (Q) divided by the area (A). We use the converted values.

\[ \begin{aligned} V &= \frac{Q}{A} \\ &= \frac{0.713 \text{ ft}^3/\text{s}}{0.0871 \text{ ft}^2} \\ &\approx 8.19 \text{ ft/s} \end{aligned} \]

The water velocity in the pipe is approximately 8.19 ft/s.

Reynolds Number (Re) Calculation

Finally, we calculate the Reynolds number (Re) to determine the flow regime, using velocity (V), diameter (D), and kinematic viscosity (\(\nu\)).

\[ \begin{aligned} Re &= \frac{V \cdot D}{\nu} \\ &= \frac{8.19 \text{ ft/s} \times 0.333 \text{ ft}}{1.08 \times 10^{-5} \text{ ft}^2/\text{s}} \\ &\approx 252,500 \end{aligned} \]

The result is \(Re \approx 252,500\). Since this number is much greater than 4000, the flow is definitively turbulent.

Diagram (After Calculations)

The calculation result places us in the turbulent flow regime, characterized by chaotic streamlines and eddies.

Flow Regime Visualization
Laminar Flow (Re < 2000)Turbulent Flow (Re > 4000)(Our Case)
Analysis

The Reynolds number is 252,500, which is much higher than 4000. The flow is therefore turbulent, as expected for a typical engineering application. We must use formulas suitable for turbulent flow for the rest of the problem.

Points of Caution

The most common error here is unit management. The flow rate is in GPM and the diameter in inches. It is imperative to convert everything to standard units (ft³/s and ft) before starting the calculations.

Key Takeaways

To master this step, remember:

  • The fundamental relationship: Flow Rate = Velocity × Area (\(Q=V \cdot A\)).
  • The Reynolds number formula: \(Re = VD/\nu\).
  • The critical threshold: \(Re > 4000\) implies turbulent flow.
Did you know?

The experiment that visualized the transition between laminar and turbulent regimes was conducted in 1883 by British engineer Osborne Reynolds. He injected a fine stream of dye into water flowing through a glass tube, spectacularly showing the transition from a straight line (laminar) to chaotic eddies (turbulent).

FAQ
Why is the flow regime so important?

Because the friction laws are radically different. In laminar flow, head loss is proportional to velocity, whereas in turbulent flow, it is proportional to (approximately) the square of the velocity, which is much more significant.

What if the fluid was oil, which is much more viscous?

The kinematic viscosity \(\nu\) would be much larger. For the same flow rate, the Reynolds number would be much lower, and the flow could potentially be laminar.

Final Answer
The flow velocity is approximately 8.19 ft/s, and the Reynolds number is approximately 252,500. The flow is turbulent.
Try it yourself

Recalculate the velocity and Reynolds number if the flow rate were reduced to 80 GPM. Would the regime change?

Question 2: Darcy Friction Factor \(f\)

Principle

The Darcy friction factor \(f\) quantifies the intensity of energy loss due to friction. In turbulent flow, it depends on both the flow's turbulence (via the Reynolds number) and the pipe's surface condition (via the relative roughness).

Mini-Lesson

The Colebrook-White equation is the most accurate relationship for finding \(f\) in turbulent flow. Because it is implicit (\(f\) is on both sides), it cannot be solved directly. We use either numerical methods (iteration) or diagrams like the Moody diagram, which is a graphical representation of this equation.

Pedagogical Note

Don't be intimidated by the complexity of the Colebrook equation. Understand what it represents: a trade-off between the effect of viscosity (the Reynolds number term) and the effect of roughness (the k/D term). For very high Reynolds numbers, the flow is "fully turbulent," and \(f\) depends almost entirely on the roughness.

Standards

The Colebrook-White equation, although empirical, is the basis for most modern fluid dynamics calculations and is the foundation of the industry-standard Moody diagram.

Formula(s)

Colebrook-White Equation

\[ \frac{1}{\sqrt{f}} = -2 \log_{10}\left(\frac{k/D}{3.7} + \frac{2.51}{Re \sqrt{f}}\right) \]
Assumptions

We assume the provided roughness value \(k\) for PVC is accurate and constant over the entire pipe length. We also assume the pipe is new.

Given Data
ParameterSymbolValueUnit
PVC Roughness\(k\)0.000005\(\text{ft}\)
Internal Diameter\(D\)0.333\(\text{ft}\)
Reynolds Number\(Re\)252,500-
Tips

To avoid iteration, you can use explicit approximations like the Swamee-Jain equation, which is very accurate: \(f = 0.25 / [\log_{10}(k/(3.7D) + 5.74/Re^{0.9})]^2\). It gives a result almost identical to Colebrook for most applications.

Diagram (Before Calculations)

The following diagram represents the roughness \(k\) on the inner surface of the pipe with diameter \(D\).

Relative Roughness
DkRelative Roughness = k/D
Calculation(s)

Relative Roughness Calculation

The Colebrook equation uses relative roughness, which is the dimensionless ratio of roughness (k) to diameter (D).

\[ \begin{aligned} \frac{k}{D} &= \frac{0.000005 \text{ ft}}{0.333 \text{ ft}} \\ &= 0.000015 \end{aligned} \]

This very low value confirms that the pipe is hydraulically smooth.

Solving Colebrook-White by Iteration

The Colebrook equation is implicit. We solve it by iteration. We start by guessing a value for \(f\), for example \(f_0 = 0.02\), and plug it into the right side of the equation to find a new value \(f_1\).

Iteration 1

\[ \begin{aligned} \frac{1}{\sqrt{f_1}} &= -2 \log_{10}\left(\frac{k/D}{3.7} + \frac{2.51}{Re \sqrt{f_0}}\right) \\ \frac{1}{\sqrt{f_1}} &= -2 \log_{10}\left(\frac{0.000015}{3.7} + \frac{2.51}{252,500 \sqrt{0.02}}\right) \\ &= -2 \log_{10}\left(4.054 \times 10^{-6} + 7.02 \times 10^{-5}\right) \\ &= -2 \log_{10}\left(7.425 \times 10^{-5}\right) \\ &\approx 8.258 \\ \Rightarrow f_1 &= \left(\frac{1}{8.258}\right)^2 \approx 0.01467 \end{aligned} \]

Our first estimate \(f_1\) is 0.01467.

Iteration 2

We repeat the process: plug this new value \(f_1 = 0.01467\) into the right side of the equation to find \(f_2\).

\[ \begin{aligned} \frac{1}{\sqrt{f_2}} &= -2 \log_{10}\left(\frac{k/D}{3.7} + \frac{2.51}{Re \sqrt{f_1}}\right) \\ \frac{1}{\sqrt{f_2}} &= -2 \log_{10}\left(\frac{0.000015}{3.7} + \frac{2.51}{252,500 \sqrt{0.01467}}\right) \\ &= -2 \log_{10}\left(4.054 \times 10^{-6} + 8.19 \times 10^{-5}\right) \\ &= -2 \log_{10}\left(8.595 \times 10^{-5}\right) \\ &\approx 8.131 \\ \Rightarrow f_2 &= \left(\frac{1}{8.131}\right)^2 \approx 0.01513 \end{aligned} \]

We get \(f_2 \approx 0.01513\). The values are very close. We can stop iterating and use this value, which we'll round to \(f \approx 0.015\) for the subsequent calculations.

Diagram (After Calculations)

The Moody diagram helps visualize this result. We find our Reynolds number on the horizontal axis, move up to the curve matching our relative roughness, and then read the \(f\) value on the vertical axis.

Position on the Moody Diagram
Refk/D = 0.000015252,5000.015
Analysis

A friction factor \(f\) of 0.015 is typical for new PVC pipes under these flow conditions. It's a low value, confirming that PVC is a hydraulically "smooth" material. For rougher materials like concrete or corroded steel, \(f\) would be significantly higher.

Points of Caution

The main error is using roughness `k` in inches or mm instead of feet. All units in the Colebrook equation (except for the dimensionless Re) must be consistent (i.e., `k` and `D` must both be in feet).

Key Takeaways

  • In turbulent flow, \(f\) depends on both Re and k/D.
  • The Colebrook equation is the standard for calculating \(f\).
  • The smoother the pipe (low k) and the more turbulent the flow (high Re), the lower \(f\) will be.

Did you know?

The Moody diagram, published in 1944 by Lewis Ferry Moody, was a revolution for engineers. It provided a graphical way to solve the complex Colebrook-White equation, which was essential before the age of calculators.

FAQ
What happens if the pipe ages?

Over time, slime or scale deposits can form, increasing the effective roughness \(k\). Consequently, the friction factor \(f\) increases, and so do the head losses for the same flow rate.

Is this `f` the same as the "Fanning" friction factor?

No. This is the Darcy (or Darcy-Weisbach) friction factor. The Fanning friction factor, `f_F`, is `1/4` of the Darcy factor (`f_F = f/4`). Always check which one your formula uses!

Final Answer
The Darcy friction factor \(f\) is approximately 0.015.
Try it yourself

Calculate the new friction factor \(f\) if the pipe were new cast iron (\(k = 0.00085 \text{ ft}\)).

Question 3: Friction Head Loss \(h_f\)

Principle

Now that we have all the components (velocity, diameter, length, friction factor), we can directly apply the Darcy-Weisbach formula to quantify the energy lost solely due to friction over the 160-foot pipe length.

Mini-Lesson

The head loss \(h_f\) represents a loss of energy per unit weight of the fluid. This is why it has units of length (feet). It can be directly converted to pressure loss (\(\Delta P\)) using the relation \(\Delta P = \gamma h_f\), where \(\gamma\) is the specific weight of the fluid (\(62.4 \text{ lb/ft}^3\) for water).

Pedagogical Note

Think of friction head loss as an "energy slope." If you were to plot the energy grade line (EGL) along the pipe, it would slope downward at a constant, steady rate. This is the slope that pumps must overcome to maintain flow.

Standards

The Darcy-Weisbach equation is one of the most fundamental equations in hydraulics. It is universally recognized and forms the basis of all head loss calculations in engineering standards and design software.

Formula(s)

Darcy-Weisbach Equation

\[ h_f = f \frac{L}{D} \frac{V^2}{2g} \]
Assumptions

We assume that the flow conditions (velocity, diameter) and pipe properties (\(f\)) are constant over the entire length L.

Given Data
ParameterSymbolValueUnit
Friction factor\(f\)0.015-
Length\(L\)160\(\text{ft}\)
Diameter\(D\)0.333\(\text{ft}\)
Velocity\(V\)8.19\(\text{ft/s}\)
Gravity\(g\)32.2\(\text{ft/s}^2\)
Tips

The term \(V^2/(2g)\) is called the "velocity head." It represents the kinetic energy of the fluid. It's useful to calculate it once, as it is used for both friction and minor losses. This simplifies the calculations.

Diagram (Before Calculations)

The following diagram illustrates how the energy grade line (EGL) drops along a straight pipe due to friction head loss.

Illustration of Friction Head Loss
Energy Grade Line (EGL)H1H2h_f
Calculation(s)

Velocity Head Calculation

The term \(V^2 / (2g)\) is the velocity head. We'll calculate it first since it's used for both major and minor losses.

\[\begin{aligned} \frac{V^2}{2g} &= \frac{(8.19 \text{ ft/s})^2}{2 \times 32.2 \text{ ft/s}^2} \\ &= \frac{67.076}{64.4} \\ &\approx 1.041 \text{ ft} \end{aligned}\]

The velocity head is approximately 1.041 ft.

Friction Head Loss Calculation

Now we apply the Darcy-Weisbach formula, plugging in all known values: \(f = 0.015\), \(L = 160 \text{ ft}\), \(D = 0.333 \text{ ft}\), and the velocity head \(V^2/(2g) \approx 1.041 \text{ ft}\).

\[ \begin{aligned} h_f &= f \frac{L}{D} \frac{V^2}{2g} \\ h_f &= 0.015 \times \left(\frac{160 \text{ ft}}{0.333 \text{ ft}}\right) \times (1.041 \text{ ft}) \\ &= 0.015 \times 480.48 \times 1.041 \text{ ft} \\ &= 7.207 \times 1.041 \text{ ft} \\ &\approx 7.50 \text{ ft} \end{aligned} \]

The energy loss due to friction over the 160 ft pipe is 7.50 ft of head.

Diagram (After Calculations)

The EGL diagram is now updated with the calculated energy loss.

Friction Head Loss Value
Energy Grade Line (EGL)H1H27.50 ft
Analysis

A loss of 7.50 feet means that to move the water over this 160-foot span, a pump would need to provide an additional pressure equivalent to a 7.50-foot column of water (about 3.25 psi), just to overcome friction.

Points of Caution

Ensure all units are consistent (feet, seconds). A common error is using the diameter in inches in the formula. Also, double-check that you are using the velocity V, not the flow rate Q, in the kinetic energy term.

Key Takeaways

  • The Darcy-Weisbach equation is the central tool for friction losses.
  • Friction losses are proportional to the length L and the square of the velocity V.
  • The result \(h_f\) is a height (energy per unit weight), not a pressure.

Did you know?

Henry Darcy, a 19th-century French engineer, conducted experiments on water flowing through sand columns for the water supply of the city of Dijon. His work laid the foundation not only for head loss calculations in pipes but also for all of modern hydrogeology (Darcy's Law).

FAQ
How do I convert this head loss to pressure loss?

Use the formula \(\Delta P = \gamma h_f\), where \(\gamma = 62.4 \text{ lb/ft}^3\). Here, \(\Delta P = 62.4 \text{ lb/ft}^3 \times 7.50 \text{ ft} = 468 \text{ lb/ft}^2\). To get PSI (pounds per square inch), divide by 144 in²/ft²: \(468 / 144 \approx 3.25 \text{ psi}\).

Is this loss significant?

It depends on the application. For a long-distance pumping system, it is a significant value to account for. For a short section, it might be negligible.

Final Answer
The friction (major) head loss over 160 ft is approximately 7.50 ft of head.
Try it yourself

What would the friction head loss be if the pipe were 640 feet long instead of 160?

Question 4: Minor Head Loss \(h_m\) (System B)

Principle

System B contains fittings (elbows and a valve) that create local turbulence, generating additional energy losses. We must sum the dimensionless loss coefficients (K) for each fitting to get a total K-value, then use the minor loss formula which relates this loss to the fluid's kinetic energy.

Mini-Lesson

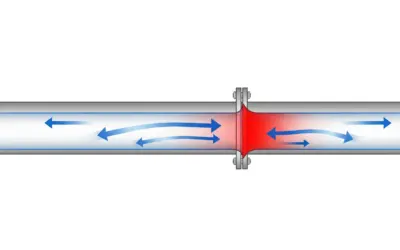
The loss coefficient K is an empirical value, determined in a lab. It represents the multiple of the velocity head (\(V^2/2g\)) that is "lost" as heat and turbulence when the fluid passes through the fitting. The more an accessory disturbs the flow (e.g., a half-closed valve), the higher its K value.

Pedagogical Note

Think of minor losses as "energy tolls." Every time the fluid encounters an obstacle, it has to "pay" a bit of its energy to pass. A straight pipe is a highway; a circuit with elbows and valves is a city road with traffic lights and intersections.

Standards

The K-values for standard fittings (elbows, tees, valves, etc.) are tabulated in numerous reference books and engineering standards, such as those from the Hydraulic Institute or in technical manuals like the Crane Technical Paper No. 410.

Formula(s)

Total Minor Head Loss

\[ h_m = \left(\sum K_i\right) \frac{V^2}{2g} \]
Assumptions

We assume the given K-values are correct and that the fittings are far enough apart that their turbulence effects do not interfere with each other.

Given Data
ParameterSymbolValueUnit
Coefficient (90° Elbow)\(K_{\text{elbow}}\)0.9-
Coefficient (Open Valve)\(K_{\text{valve}}\)0.2-
Velocity Head\(V^2/2g\)1.041\(\text{ft}\)
Tips

An alternative method for minor losses is the "equivalent length" (L_e) method. Each fitting is equated to a certain length of straight pipe that would produce the same loss (L_e = K * D / f). It's just another way of presenting the same calculation.

Diagram (Before Calculations)

Passing through an elbow forces the streamlines to bend, creating a separation zone and turbulence that dissipates energy.

Turbulence in an Elbow
TurbulenceZone
Calculation(s)

Sum of K-Coefficients

To calculate the total minor loss, we first sum the K-values for all fittings in System B: two 90° elbows (\(K=0.9\)) and one open valve (\(K=0.2\)).

\[ \begin{aligned} \sum K_i &= K_{\text{elbow1}} + K_{\text{elbow2}} + K_{\text{valve}} \\ &= 0.9 + 0.9 + 0.2 \\ &= 2.0 \end{aligned} \]

The total minor loss coefficient for this circuit is \(\sum K_i = 2.0\).

Minor Head Loss Calculation

We then use the minor loss formula, multiplying this total K-value by the velocity head (\(V^2/2g \approx 1.041 \text{ ft}\)) that we already calculated in Question 3.

\[ \begin{aligned} h_m &= \left(\sum K_i\right) \frac{V^2}{2g} \\ h_m &= 2.0 \times \left( \frac{(8.19 \text{ ft/s})^2}{2 \times 32.2 \text{ ft/s}^2} \right) \\ &\approx 2.0 \times 1.041 \text{ ft} \\ &\approx 2.08 \text{ ft} \end{aligned} \]

The energy loss due to the three fittings is 2.08 ft of head.

Diagram (After Calculations)

The energy grade line experiences sharp drops at each fitting, corresponding to the localized energy loss.

Impact on the Energy Grade Line
KKKDrops due to minor losses
Analysis

The loss from the fittings alone (2.08 ft) is a significant portion of the friction loss (7.50 ft). This illustrates that even in a relatively long pipe, ignoring minor losses can lead to a significant underestimation of the total losses.

Points of Caution

A common error is to forget a fitting in the sum of K-values, or to grab the wrong coefficient from reference tables (e.g., a 45° elbow instead of 90°).

Key Takeaways

  • Minor losses are localized at fittings.
  • They are calculated using a K-coefficient and the velocity head \(V^2/2g\).
  • The total minor loss is the sum of the losses from each individual fitting.

Did you know?

A fully open butterfly valve or ball valve creates more head loss than a fully open gate valve of the same diameter, because their opening mechanism remains a larger obstruction in the flow path.

FAQ
Where do these K-coefficients come from?

They are determined experimentally in laboratories by fittings manufacturers or research organizations. They measure the head loss for a specific fitting under various flow conditions.

What if a valve is half-closed?

Its K-coefficient increases dramatically! A half-closed valve can have a K of 5, 10, or even higher, easily becoming the dominant source of head loss in the entire system.

Final Answer
The total minor (singular) head loss for System B is approximately 2.08 ft of head.
Try it yourself

What would the minor head loss be if the valve were replaced with a globe valve (\(K=10\))?

Question 5: Comparison of Total Head Loss

Principle

The total head loss (`h_L`) of a network is simply the sum of the friction (major) losses (`h_f`) and the minor losses (`h_m`). By comparing the totals for both systems, we can quantify the real-world impact of adding a few elbows and a valve.

Mini-Lesson

The general energy equation (or extended Bernoulli's equation) states that the energy at point 1 equals the energy at point 2, plus any energy added by a pump (pump head), minus the energy lost (total head loss, `h_L`). Calculating \(h_L\) is therefore essential for determining the required pump power for a system.

Pedagogical Note

This final calculation is the synthesis of the entire exercise. It shows that network design is a trade-off. System A is more energy-efficient, but System B might be necessary to bypass an obstacle. The engineer must then quantify the energy "cost" of this geometric constraint.

Standards

The principle of adding friction and minor losses is a standard approach in all hydraulic network design methodologies. Professional simulation software applies this same fundamental principle.

Formula(s)

Total Head Loss

\[ h_L = h_f + h_m \]
Assumptions

We assume there is no elevation change between the inlet and outlet of the systems so that the comparison focuses solely on friction and minor losses.

Given Data
ParameterSymbolValueUnit
Calculated Friction Loss\(h_f\)7.50\(\text{ft}\)
Minor Loss (System B)\(h_{m, B}\)2.08\(\text{ft}\)
Tips

To quickly estimate the relative importance of losses, you can compare the sum of K-values (\(\sum K\)) to the friction term (\(f L/D\)). If \(\sum K\) is in the same order of magnitude as \(f L/D\), minor losses are significant. If \(f L/D\) is much larger, they are likely negligible.

Diagram (Before Calculations)

The following diagram conceptualizes the addition of friction and minor losses to get the total loss.

Composition of Total Head Loss
h_f (Friction)+h_m (Minor)=h_L (Total)
Calculation(s)

Total Loss for System A

The total loss for System A (straight pipe) is the sum of its friction loss (calculated in Q3) and its minor loss (which is zero, as there are no fittings).

\[ \begin{aligned} h_{L, A} &= h_f + h_{m, A} \\ &= 7.50 + 0 \\ &= 7.50 \text{ ft} \end{aligned} \]

Total Loss for System B

The total loss for System B is the sum of its friction loss (which is identical to System A, as the length L=160ft is the same) and its minor loss (calculated in Q4).

\[ \begin{aligned} h_{L, B} &= h_f + h_{m, B} \\ &= 7.50 + 2.08 \\ &= 9.58 \text{ ft} \end{aligned} \]

Percentage Increase Calculation

Finally, we calculate the percentage increase by comparing the difference in loss between the two systems (\(9.58 - 7.50\)) to the loss of the baseline system (System A).

\[ \begin{aligned} \text{Increase} (\%) &= \frac{h_{L, B} - h_{L, A}}{h_{L, A}} \times 100 \\ &= \frac{9.58 - 7.50}{7.50} \times 100 \\ &= \frac{2.08}{7.50} \times 100 \\ &\approx 27.7\% \end{aligned} \]

Adding two elbows and a valve increased the total energy loss by 27.7%.

Diagram (After Calculations)

The chart clearly shows that the total head loss for System B is greater than for System A, with the increase entirely due to the red "Minor Loss" bar.

Head Loss Comparison
Analysis

Adding just three fittings increased the total energy loss by over 27%. This shows that minor losses, while localized, should never be neglected in hydraulic network design. They can have a considerable energy impact, translating directly to higher pump energy consumption.

Points of Caution

Don't compare apples to oranges. Ensure that the total length and diameter are the same for both systems so that the only variable being tested is the presence of fittings.

Key Takeaways

  • Total head loss is the sum of friction (major) and minor losses.
  • Fittings can account for a very large portion of the total energy loss, especially in short, complex networks.
  • Optimizing a pipe layout to minimize bends and fittings is an effective strategy for reducing energy consumption.

Did you know?

In HVAC (Heating, Ventilation, and Air Conditioning) systems in large buildings, the ductwork networks are so complex (elbows, tees, dampers, filters) that minor losses often account for more than 75% of the total system head loss.

FAQ
When is it truly acceptable to neglect minor losses?

In very long pipelines (oil pipelines, water transmission lines over many miles). In those cases, the \(f L/D\) term becomes so large that the \(\sum K\) term is negligible in comparison. Conversely, in a boiler room, minor losses are dominant.

How does this calculation influence pump selection?

The pump must provide a total dynamic head (TDH) at least equal to the total head loss of the network (plus any static elevation change). A 27.7% increase in head loss could require selecting the next size up for a pump, making it more expensive to buy and operate.

Final Answer
The total head loss is 7.50 ft for System A and 9.58 ft for System B. The fittings cause a 27.7% increase in total head loss.
Try it yourself

If the pipe were only 32 ft long instead of 160 ft, what would the new percentage increase be from the fittings?

Interactive Tool: Head Loss Simulator

Use the sliders to vary the flow rate and pipe diameter (for System B) and observe the impact on velocity, flow regime, and head loss.

Input Parameters
320 GPM
4.0 in
Key Results (System B)
Velocity (ft/s) -
Reynolds Number -
Total Head Loss (ft) -

Final Quiz: Test Your Knowledge

1. If you double the flow rate in a pipe, what happens to the approximate friction head loss?

2. What is the main characteristic of a laminar flow regime?

3. In the Darcy-Weisbach equation, the friction factor \(f\) depends on:

4. What does a "minor" head loss refer to?

5. To reduce friction head loss in an existing system without changing the flow rate, the most effective solution is:

Glossary

Head Loss
Represents the energy dissipation (pressure loss) of a moving fluid in a pipe. It is expressed in Pascals (Pa) or, more commonly, in feet of fluid head.
Reynolds Number (Re)
A dimensionless quantity used in fluid mechanics to characterize a flow regime. It helps predict whether the flow will be laminar or turbulent.
Roughness (k)
A measure of the texture of a pipe's inner surface. High roughness increases friction and thus friction head loss.
Friction Head Loss (Major Loss)
Energy loss due to the fluid's friction against the pipe walls over its entire length. Also called major or linear loss.
Minor Head Loss
Localized energy loss caused by flow disturbance when passing through a fitting (elbow, valve, tee, expansion, etc.). Also called singular loss.
Exercise: Comparing Hydraulic Head Loss
Total Head Loss in a Simple Pipe System
Total Head Loss in a Simple Pipe System

Exercise: Total Head Loss in a Simple Pipe System Calculating Total Head Loss in a Simple Pipe System Context: Water Flow in Pipes. In hydraulics, particularly in civil engineering fields like potable water supply or sanitation systems, it is crucial to understand and...

Calculating Singular Head Loss for a Valve
Calculating Singular Head Loss for a Valve

Exercise: Singular Head Loss for a Valve Calculating Singular Head Loss for a Valve Context: Singular Head LossLocalized energy losses in a hydraulic circuit, caused by pipe fittings (elbows, valves, tees, etc.) that disrupt the fluid flow.. In any hydraulic circuit,...

EGL and HGL Calculation
EGL and HGL Calculation

Exercise: EGL and HGL Calculation Calculating the Energy Grade Line (EGL) and Hydraulic Grade Line (HGL) Context: The study of pressurized pipe flowFlow of a fluid that completely fills a closed conduit. The pressure can be greater or less than atmospheric pressure.....

Head Loss Calculation with Hazen-Williams
Head Loss Calculation with Hazen-Williams

Exercise: Head Loss Calculation with Hazen-Williams Head Loss Calculation with Hazen-Williams Context: Sizing a Water Supply Pipeline. One of the major challenges in hydraulic engineering is transporting water over long distances efficiently. To do this, it's crucial...

Influence of Viscosity on Head Loss
Influence of Viscosity on Head Loss

Influence of Viscosity on Head Loss (US Customary Units) Influence of Viscosity on Head Loss Context: Fluid Flow in Pipes. Transporting fluids (water, oil, gas, etc.) through pipelines is ubiquitous in industry and daily life. During this flow, the fluid rubs against...

Total Head Loss in a Simple Pipe System
Total Head Loss in a Simple Pipe System

Exercise: Total Head Loss in a Simple Pipe System Calculating Total Head Loss in a Simple Pipe System Context: Water Flow in Pipes. In hydraulics, particularly in civil engineering fields like potable water supply or sanitation systems, it is crucial to understand and...

Calculating Singular Head Loss for a Valve
Calculating Singular Head Loss for a Valve

Exercise: Singular Head Loss for a Valve Calculating Singular Head Loss for a Valve Context: Singular Head LossLocalized energy losses in a hydraulic circuit, caused by pipe fittings (elbows, valves, tees, etc.) that disrupt the fluid flow.. In any hydraulic circuit,...

EGL and HGL Calculation
EGL and HGL Calculation

Exercise: EGL and HGL Calculation Calculating the Energy Grade Line (EGL) and Hydraulic Grade Line (HGL) Context: The study of pressurized pipe flowFlow of a fluid that completely fills a closed conduit. The pressure can be greater or less than atmospheric pressure.....

Head Loss Calculation with Hazen-Williams
Head Loss Calculation with Hazen-Williams

Exercise: Head Loss Calculation with Hazen-Williams Head Loss Calculation with Hazen-Williams Context: Sizing a Water Supply Pipeline. One of the major challenges in hydraulic engineering is transporting water over long distances efficiently. To do this, it's crucial...

Influence of Viscosity on Head Loss
Influence of Viscosity on Head Loss

Influence of Viscosity on Head Loss (US Customary Units) Influence of Viscosity on Head Loss Context: Fluid Flow in Pipes. Transporting fluids (water, oil, gas, etc.) through pipelines is ubiquitous in industry and daily life. During this flow, the fluid rubs against...

0 Comments
Submit a Comment

Your email address will not be published. Required fields are marked *